Research

Supersonic Flow and Hydraulic Jump in an Electronic de Laval Nozzle

Johannes Geurs, Tatiana A. Webb, Yinjie Guo, Itai Keren, Jack H. Farrell, Jikai Xu, Kenji Watanabe, Takashi Taniguchi, et al.

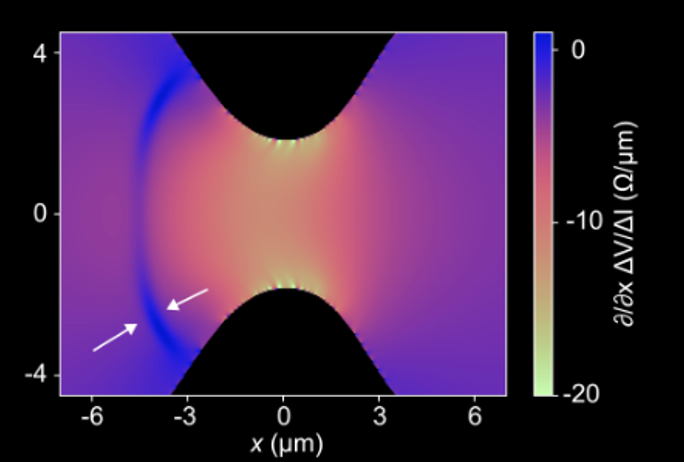
We demonstrate compressible electron flow in bilayer graphene through an electronic de Laval nozzle, accelerating charge carriers past the electronic speed of sound until they slow down suddenly in a shock. Discontinuities in transport and local potential measurements provide evidence of a viscous electron shock front and supersonic flow, opening the door for novel, intrinsically nonlinear electronic devices beyond the paradigm of incompressible flow.

Paper

Generalized Time-Reversal Symmetry and Effective Theories for Nonequilibrium Matter

Xiaoyang Huang, Jack H. Farrell, Aaron J. Friedman, Isabella Zane, Paolo Glorioso, Andrew Lucas

We develop a systematic effective theory framework for the classical stochastic dynamics of nonequilibrium systems. Using examples from nonreciprocal dynamics, driven rigid-body motion, and active chiral fluids, we demonstrate how generalized time-reversal symmetry plays a crucial role. This formalism yields generalizations of the fluctuation-dissipation theorem and provides an alternative route to building phenomenological models of driven and active matter.

Paper

Hydrodynamics with Helical Symmetry

Jack H. Farrell, Xiaoyang Huang, Andrew Lucas

We present the hydrodynamics of fluids in three spatial dimensions with helical symmetry, wherein only a linear combination of a rotation and translation is conserved in one direction. We derive nondissipative hydrodynamic coefficients, demonstrate microscopic realizations through Hamiltonian systems and kinetic theory, and explore connections to pinned cholesteric liquid crystals.

Paper

Terahertz Radiation from the Dyakonov-Shur Instability of Hydrodynamic Electrons in a Corbino Geometry

Jack H. Farrell, Nicolas Grisouard, Thomas Scaffidi

We study how hydrodynamic electrons in a Corbino disk undergo a plasma instability above a critical drift velocity, forming a coherent nonlinear oscillator. The Dyakonov-Shur instability is substantially enhanced in this geometry, offering promise as a terahertz radiation source. Our analysis combines hydrodynamic theory with linearized calculations and full numerical simulations of the Navier-Stokes equation, with direct relevance to experimental observations in graphene.

Paper